LeetCode: 142. Linked List Cycle II

解法

遍历链表，记录访问过的节点，找出环开始的节点

遍历链表，把访问过的节点都记下来，如果发现有节点指向了一个已访问过的节点，说明链表存在环，并且当前节点就是环开始的节点

这个方法的 Python 代码类似下面这样:

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        if head is None:
            return None

        seen = {}
        while head is not None:
            if head in seen:
                return head

            seen[head] = True
            head = head.next

        return None

快慢双指针方法，判断是否有环，然后再找出环开始的节点

快慢双指针判断是否有环的方法的思路是：

  • 定义快和慢两个指针，从 head 开始遍历链表，慢指针一次移动一个节点，快指针一次移动两个节点
  • 如果快指针到达了链表尾部，说明没有环（因为如果有环的话，会死循环没有尾部）
  • 如果快指针和慢指针移动到了同一个节点上，说明有环（因为如果没环的话，快指针永远在慢指针前面，有环时，因为快指针比慢指针移动的速度要快，在移动到有环的地方的时候会跑到慢指针后面去（多次移动后会出现），最终出现快慢两个指针相遇移动到同一个节点的情况（多次移动后出现））

对于有环的链表，通过下面的方法找出环开始的节点：

  • 将慢指针移动到 head 位置重新开始遍历链表，快指针继续往前移动，当快慢指针相遇时，当前节点即为环开始的节点

为啥通过这个新的快慢指针的移动可以找到环开始的节点，看一下移动轨迹：

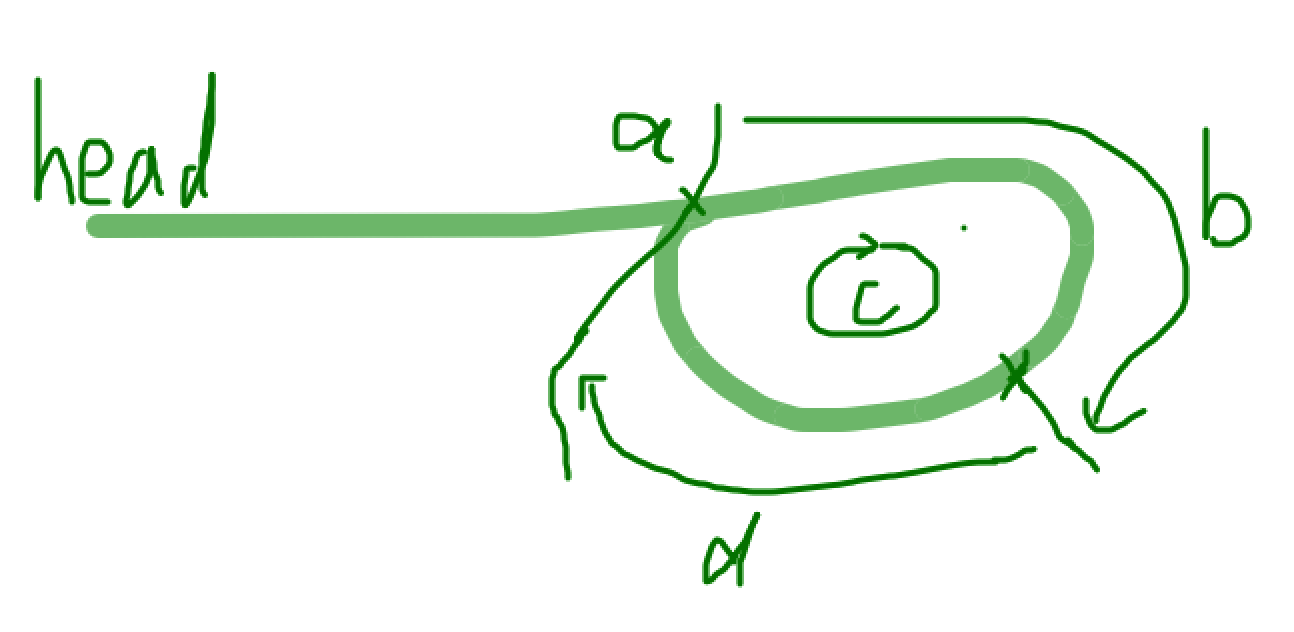
imagex

  • 假设环开始位置为 a , 第一次快慢指针相遇时，相遇位置距离环开始位置 b 步， 绕环一圈需要移动 c 步， 从 b 往前移动到环开始位置需要 d 步，快指针绕环移动了 x 圈，慢指针绕环移动了 y 圈。

  • # 快指针移动的步数是慢指针的 2 倍
a + b + x * c = 2 * (a + b + y * c)
a + b + x * c = 2a + 2b + 2y *c
x * c - 2y * c = a + b
(x - 2y) * c = a + b
a + b = (x - 2y) * c
a = (x - 2y) * c - b
#
b = c - d
a = (x - 2y) * c - (c - d)
a = (x - 2y - 1) * c + d
# 可以得出，从 head 到 a 的步数等于绕环 n 圈然后再走 d 步的步数
#
# 可以从相遇位置绕环 n 圈再走 d 步，此时刚好到达环起始位置
# 同时从 head 走 a 步也会到达环起始位置

这个方法的 Python 代码类似下面这样:

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        if head is None:
            return None

        slow, fast = head, head
        has_cycle = False

        while fast is not None and fast.next is not None:
            slow = slow.next
            fast = fast.next.next
            if fast is slow:
                has_cycle = True
                break

        if not has_cycle:
            return None

        slow = head
        while slow is not fast:
            slow = slow.next
            fast = fast.next

        return slow

Comments