LeetCode: 669. Trim a Binary Search Tree

题目

原题地址：https://leetcode.com/problems/trim-a-binary-search-tree/

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

Example 1:

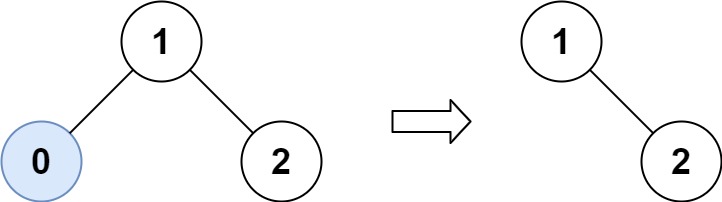
image1

Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

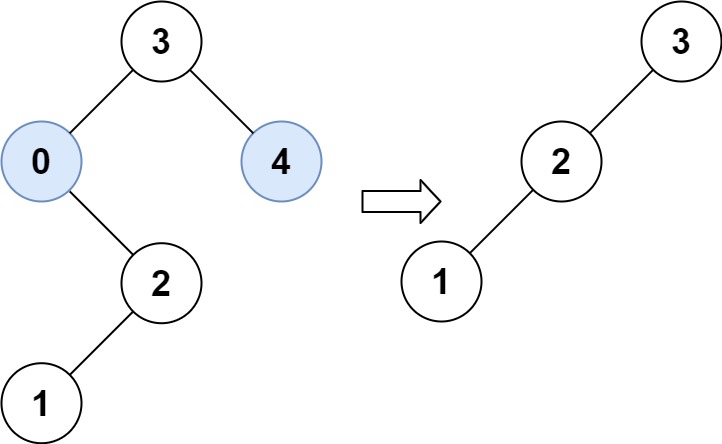
image2

Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Example 3:

Input: root = [1], low = 1, high = 2
Output: [1]

Example 4:

Input: root = [1,null,2], low = 1, high = 3
Output: [1,null,2]

Example 5:

Input: root = [1,null,2], low = 2, high = 4
Output: [2]

Constraints:

  • The number of nodes in the tree in the range [1, 104].
  • 0 <= Node.val <= 104
  • The value of each node in the tree is unique.
  • root is guaranteed to be a valid binary search tree.
  • 0 <= low <= high <= 104

解法

遍历二叉树，在遍历的过程中重建二叉树，将不满足条件的节点删除（ 节点的值必须满足 low <= value <= high ）：

  • 如果当前节点的值 < low，那么根据 BST 的特性可知，它的左子树肯定也都 < low，此时需要用右子树代替当前节点的位置。
  • 如果当前节点的值 > high，那么根据 BST 的特性可知，它的右子树肯定也都 > high，此时需要用左子树代替当前节点的位置。

这个方法的 Python 代码类似下面这样:

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def trimBST(self, root, low, high):
        if root is None:
            return

        if root.val < low:
            # 舍弃当前节点和它的左子树，因为左子树各节点的值肯定 < low
            root = self.trimBST(root.right, low, high)
        elif root.val > high:
            # 舍弃当前节点和它的右子树，因为右子树各节点的值肯定 > high
            root = self.trimBST(root.left, low, high)
        else:
            root.left = self.trimBST(root.left, low, high)
            root.right = self.trimBST(root.right, low, high)

        return root

Comments