LeetCode: 235. Lowest Common Ancestor of a Binary Search Tree

题目

原题地址：https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia : “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

image1

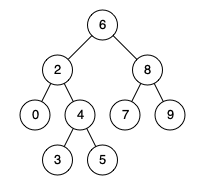
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

image2

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2

Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [2, 10^5].
  • -10^9 <= Node.val <= 10^9
  • All Node.val are unique.
  • p != q
  • p and q will exist in the BST.

题目大意是，求二叉搜索树中指定两个节点的最近共同祖先。

解法

遍历 BST，如果当前 root 节点：

  • 为 None ，则返回 None
  • 节点值等于 p 或 q 的值，则当前节点即为要找的 LCA，因为当前节点是 p 或 q 其中一个节点，不会有比它更近的共同祖先了。
  • 节点值比 p 和 q 的值都大，根据 BST 的特性，改为从当前节点的左子数中查找
  • 节点值比 p 和 q 的值都小，根据 BST 的特性，改为从当前节点的右子数中查找
  • 节点值比其中一个大，比另一个小，根据 BST 的特性，p 和 q 分别分布在当前节点的左右子数中， 当前节点即为要找的 LCA。

这个思路的 Python 代码类似下面这样：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        if root is None:
            return None

        if root.val == p.val or root.val == q.val:
            return root

        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        if root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)

        return root

Comments