LeetCode: 124. Binary Tree Maximum Path Sum

题目

原题地址： https://leetcode.com/problems/binary-tree-maximum-path-sum/

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any path.

Example 1:

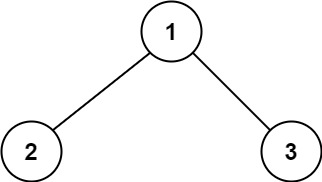
image1

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

image2

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

  • The number of nodes in the tree is in the range [1, 3 * 10^4].
  • -1000 <= Node.val <= 1000

题目大意是，求二叉树节点和最大的路径，求二叉树的最长相同值的路径，只是将相同值的条件改为了路径上节点和最大

解法

类似二叉树最长相同值路径的题，这里是求任意路径的节点值的和，不过要增加一个限制， 那就是左右子树节点和先跟 0 比较，如果 < 0 的话，就取 0 表示放弃该子树 （因为是求节点和最大值，如果加上为负的子树的话，值反而会变小，丢弃为负的子树更合理） 也就是说，如果子树的节点值的和 < 0 的话，那它们的和就取 0。

这个思路的 Python 代码类似下面这样：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        self._max_sum = -1001
        self._path_sum(root)

        return self._max_sum

    def _path_sum(self, root):
        if root is None:
            return 0

        left_sum = self._path_sum(root.left)
        right_sum = self._path_sum(root.right)

        # 如果子树的节点和 < 0，取 0 即舍弃这个子树
        if left_sum < 0:
            left_sum = 0
        if right_sum < 0:
            right_sum = 0

        sum = root.val + left_sum + right_sum
        if sum > self._max_sum:
            self._max_sum = sum

        return root.val + max(left_sum, right_sum)

Comments