LeetCode: 337. House Robber III

题目

原题地址： https://leetcode.com/problems/house-robber-iii/

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example 1:

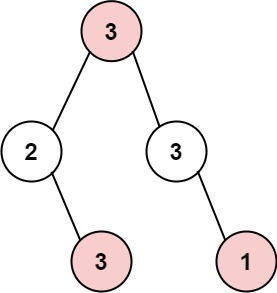
image1

Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

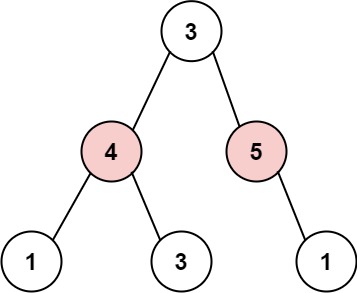
image2

Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].
  • 0 <= Node.val <= 10^4

题目大意是，从所有不相邻的节点的组合中找出节点值和最大的那个组合的和值

解法

一个方法是暴力尝试所有可能：

  • 对于每个 root 节点，只有两个可能：组合中包括 root 节点、组合中不包括 root 节点
  • 如果包括 root 节点，那么： * 最大和就等于 root.val + 左子数的子树的最大和 + 右子树的子树的最大和 * 因为限制了节点不能相邻，所以上面是左子数的子树和右子树的子树而不是左子数和右子树
  • 如果不包括 root 节点，那么： * 最大和就等于左子数的最大和 + 右子树的最大和
  • 比较两个可能得出的最大和，取更大的值作为答案

可以通过递归实现上面的思路，因为对每个节点都需要做递归尝试两个可能，期间就会有重复的计算， 可以保存一下中间值节省时间。

这个思路的 Python 代码类似下面这样：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def rob(self, root):
        self._max_sum = 0
        self._tmp_store = {}

        return self._helper(root)

    def _helper(self, root):
        if root is None:
            return 0

        if root in self._tmp_store:
            return self._tmp_store[root]

        # 包括 root
        include_root_left = 0
        include_root_right = 0
        if root.left is not None:
            include_root_left = self._helper(root.left.left) + \
                                self._helper(root.left.right)
        if root.right is not None:
            include_root_right = self._helper(root.right.left) + \
                                 self._helper(root.right.right)
        include_root_sum = root.val + include_root_left + include_root_right

        # 不包括 root
        skip_root_left = self._helper(root.left)
        skip_root_right = self._helper(root.right)
        skip_root_sum = skip_root_left + skip_root_right

        _sum = max(include_root_sum, skip_root_sum)
        self._tmp_store[root] = _sum

        return _sum

Comments