LeetCode: 590. N-ary Tree Postorder Traversal

题目

原题地址：https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/

Given a binary tree, return the vertical order traversal of its nodes values.

For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).

Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).

If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.

Return an list of non-empty reports in order of X coordinate. Every report will have a list of values of nodes.

Example 1:

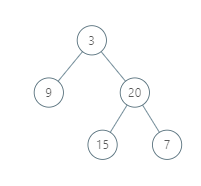
image

Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation:
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).

Example 2:

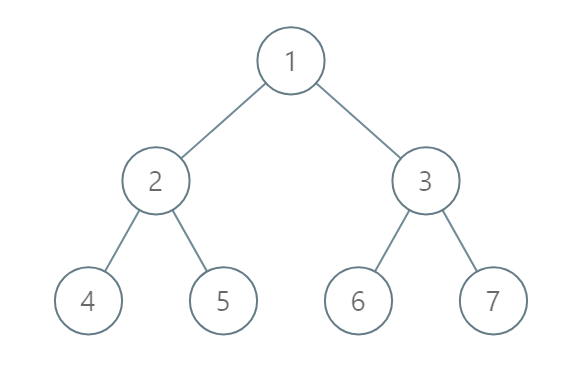
image2

Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.

Note:

  • The tree will have between 1 and 1000 nodes.
  • Each node's value will be between 0 and 1000.

解法

计算每个节点的 (x, y) 坐标，然后按 x 轴的值排序， 遍历排序后的结果，x 轴值相等的节点在同一条垂直线上可以归为一组。

这个方法的 Python 代码类似下面这样:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def verticalTraversal(self, root):
        self._positions = []
        self._collect_positions(root, 0, 0)

        vals = []
        last_x = -1001
        for x, y, val in sorted(self._positions):
            # x 轴值相同的归为一组
            if x != last_x:
                vals.append([])
                last_x = x

            vals[-1].append(val)

        return vals


    def _collect_positions(self, root, x, y):
        if root is None:
            return

        self._positions.append((x, y, root.val))

        # 之所以是 y + 1 而不是 y - 1 是为了实现排序后低层级的在前面
        self._collect_positions(root.left, x - 1, y + 1)
        self._collect_positions(root.right, x + 1, y + 1)

Comments